Poisson’s Ratio – My DataBook

Summary

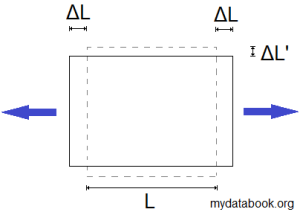
When a material is stretched in one direction, it will usually shrink in the other perpendicular directions.

The Poisson’s ratio, $v$ , is the ratio of transverse strain, $\epsilon_t$ to axial strain $\epsilon_a$ , where an axial force has been applied.

(1) $\begin{align*}v = -\frac{\epsilon_t}{\epsilon_a}\end{align*}$

The strain of a material is defined as:

(2) $\begin{align*}\epsilon = \frac{\Delta L}{L}\end{align*}$

Where $\Delta L$ = change in length, $L$ = original length.

2D Poisson Ratio

Poisson’s ratio will typically be between 0 to 0.5 for most common materials.

Approximation for Very Small Strains

For very small changes in length, an approximation for Poisson’s ratio is:

(3) $\begin{align*}v \approx\frac{\Delta\L'}{\Delta\L}\end{align*}$

Typical Poisson’s Ratios for Common Materials