Reynold’s Number

Reynold’s Number

Summary

The Reynold’s number is a dimensionless number that characterises the flow of a fluid and is represented by:

(1)   \begin{align*}Re = \frac{\rho u D\x_H}{\mu}\end{align*}

Where Re = Reynold’s number, \rho = density, u = fluid velocity, D\x_H = characteristic length or hydraulic diameter, \mu = dynamic viscosity. It can be alternatively written in terms of the kinematic visocity:

(2)   \begin{align*}Re = \frac{u L}{v}\end{align*}

Where v = kinematic visocity and is equivalent to v = \frac{\mu}{\rho}.

The Reynold’s Number characterises the flow as laminar when Re < 2000, as transient when 2000 < Re < 4000 and as turbulent when Re > 4000.

Characteristic Length / Hydraulic Diameter

The characteristic length, also known as the hydraulic diameter, is the ratio of cross-sectional area to the ‘wetted’ perimeter of the tube or channel the flow is moving through. It is defined as:

(3)   \begin{align*}D\x_H = \frac{4A}{P}\end{align*}

Where A = cross-sectional area and P = perimeter of the channel or tube in contact with the fluid.

For example, the characteristic length for a fully filled tube with internal diameter, D, is:

(4)   \begin{align*}D\x_H = \frac{4(\pi D^2 / 4)}{\pi D} = D\end{align*}

For a fully filled square channel with side length, L, the characteristic length is:

(5)   \begin{align*}D\x_H = \frac{4L^2}{4L} = L\end{align*}

A partially filled rectangular open channel with width, a, and height, b, is shown below:

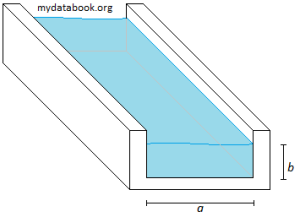
Open Channel with Fluid

Here, only 3 surfaces are in contact with the fluid and are ‘wetted’. The ‘wetted’ perimeter is therefore only (a + 2b). As such the the characteristic length is:

(6)   \begin{align*}D\x_H = \frac{4ab}{a + 2b}\end{align*}

Reynold’s Number Calculator from Dynamic Viscosity

Calculate Reynold’s number from Dynamic Viscosity
Formula: Re = \frac{\rho u D\x_H}{\mu}

Re = Reynold’s number

\rho = density

u = fluid velocity

D\x_H = characteristic length

\mu = dynamic viscosity
Density  kg/m³
Fluid velocity  m/s
Characteristic Length m
Dynamic Viscosity m²/s
Result:

Reynold’s Number Calculator from Kinematic Viscosity

Calculate Reynold’s number from Kinematic Viscosity
Formula: Re = \frac{ u D\x_H}{v}

Re = Reynold’s number

u = fluid velocity

D\x_H = characteristic length

v = kinematic viscosity
Fluid velocity  m/s
Characteristic Length m
Kinematic Viscosity m²/s
Result: